[空间几何体教学反思]篇一 近来有点忙,很长时间没有更新博客了。 今天受青岛一所学校校长之约,来青岛与这所学校的老师交流教学体会。晚上有点时间,正好宾馆可以上网,写写近期的一些教学感想。 前面...+阅读
数学立体几何的空间向量法是理科内容,文科才会不讲。 按照道理,高二结束应该学习完毕了,没学的不会考。 空间向量作为新加入的内容,在处理空间问题中具有相当的优越性,比原来处理空间问题的方法更有灵活性。 如把立体几何中的线面关系问题及求角求距离问题转化为用向量解决,如何取向量或建立空间坐标系,找到所论证的平行垂直等关系,所求的角和距离用向量怎样来表达是问题的关键. 立体几何的计算和证明常常涉及到二大问题:一是位置关系,它主要包括线线垂直,线面垂直,线线平行,线面平行;二是度量问题,它主要包括点到线、点到面的距离,线线、线面所成角,面面所成角等。 这里比较多的主要是用向量证明线线、线面垂直及计算线线角,而如何用向量证明线面平行,计算点到平面的距离、线面角及面面角的例题不多,起到一个抛砖引玉的作用。 以下用向量法求解的简单常识:
1、空间一点P位于平面MAB的充要条件是存在唯一的有序实数对x、y,使得 或对空间一定点O有
2、对空间任一点O和不共线的三点A,B,C,若: (其中x+y+z=1),则四点P、A、B、C共面.
3、利用向量证a‖b,就是分别在a,b上取向量 (k∈R).
4、利用向量证在线a⊥b,就是分别在a,b上取向量 .
5、利用向量求两直线a与b的夹角,就是分别在a,b上取 ,求: 的问题.
6、利用向量求距离就是转化成求向量的模问题: .
7、利用坐标法研究线面关系或求角和距离,关键是建立正确的空间直角坐标系,正确表达已知点的坐标. 首先该图形能建坐标系 如果能建 则先要会求面的法向量 求面的法向量的方法是 1。 尽量在土中找到垂直与面的向量 2。如果找不到,那么就设n=(x,y,z) 然后因为法向量垂直于面 所以n垂直于面内两相交直线 可列出两个方程 两个方程,三个未知数 然后根据计算方便 取z(或x或y)等于一个数 然后就求出面的一个法向量了 会求法向量后 1。 二面角的求法就是求出两个面的法向量 可以求出两个法向量的夹角为两向量的数量积除以两向量模的乘积 如过在两面的同一边可以看到两向量的箭头或箭尾相交 那么二面角就是上面求的两法向量的夹角的补角 如果只能看到其中一个的箭头和另一个的箭尾相交 那么上面两向量的夹角就是所求 2。 点到平面的距离就是求出该面的法向量 然后在平面上任取一点(除平面外那点在平面内的射影) 求出平面外那点和你所取的那点所构成的向量记为n1 点到平面的距离就是法向量与n1的数量积的绝对值除以法向量的模即得所求。
延伸阅读:
饺子的七种包法怎么做1. 胶东鲅鱼饺子~~~~这个饺子的个头你可以想象下,一般饭店里包得比我这个大两倍 外地人第一次看到都会惊叹的~~~吃几个就饱 十种家常饺子包法的做法图解22. 两边捏合即可~~~~...
立体手工剪纸新年贺卡背景教人怎么做新年卡片如何制作——制作元旦就要到啦,一起来做亲子手工啦。怎样手工制作一张简单又可爱的元旦立体贺卡呢?元旦元旦,当然要有可爱的蛋蛋啦。 工具/原料 卡纸 彩色纸 爱心、星...
怎样才能学好空间几何立体几何就是考察你的空间想像力,首先书上的所有定理你都理解并记下了没如果没有,请先把这一点做到题目中一般有以下几个问题: (1)证明线与线的关系: 书上的定理直接证 在一个平面...
怎样学好高中空间几何立体几何的题目是的确很简单的,主要是你要能够想象到几何体的空间构型,几何体上点极其直线的位置关系,一些解题时常用的作辅助线的方法,记住书上的定理和结论,将它们灵活的运用。...
高三数学解析几何设M(x1,y1),N(x2,y2),Q(1,0),依题意,直线PA经过点A(-2,0),P(4,t),可以设AP:y=t6(x+2),(6分) 和圆x2+y2=4联立,得到y=t6(x+2)x2+y2=4,代入消元得到,(t2+36)x2+4t2x+4t2-144=0,(7分)...
一道高中数学立体几何的题目这应该是高中数学的附加题吧,(1)用基本方法,建系,找点坐标,代入计算。。(2)做fo垂直于mn于o点,然后求fo,mo长,最后勾股定理。 所以A'在ABCD上的投影是交点 不好意思,我看错了,你再等等,我...
求有关高中立体几何的数学题三角形ABC在平面a之外,AB∩a=P,BC∩a=Q,AC∩a=R,求证:P、Q、R三点共线。 解: 设三角形ABC所在的平面为b,由“一条直线上,若有两点在一个平面能,则该直线必在该平面内”知,直线AB,AC,...
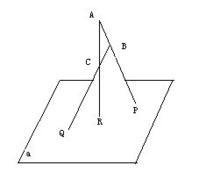
一道高中数学立体几何题解:(1):D,E是点A在PB,PC的射影。 ∴AD⊥PB,AE⊥PC ∠ABC=90° ∴CB⊥AB ① 且 ∵PA⊥平面ABC ∴PA⊥CB ② 结合①,②可得 CB⊥PAB ∴CB⊥AD 又 AD⊥PB ∴AD⊥平面PBC DE在平面PB...
高中数学立体几何题底面是正三角形,顶点在底面的射影是底面三角形的中心的三棱锥 根据定义来就行了! 1,4,可以证明,三个侧棱相等.且顶点在底面的射影是底面三角形的中心(由于是正三角形,四心合一). 2:...





