[三角形有关的线段教学反思]教学反思范文一: 本课题设计思路按操作、猜想、验证的学习过程,遵循从感性到理性的渐进认识规律,暴露了知识发生过程,体现了数学学习的必然性.教学先从学生折纸开始,让学生体验三...+阅读
怎样去计算锐角三角形直角三角形钝角三角形的面积
初中数学锐角三角函数通常作为选择题,填空题和应用题压轴题出现,考察同学们灵活运用公式和定理能力,是中考一大难点之一。初中数学锐角三角函数知识点一览:锐角三角函数定义,正弦(sin),余弦(cos)和正切(tan)介绍,锐角三角函数公式(特殊三角度数的特殊值,两角和公式半角公式,和差化积公式),锐角三角函数图像和性质,锐角三角函数综合应用题。
一、锐角三角函数定义 锐角三角函数是以锐角为自变量,以此值为函数值的函数。如图:我们把锐角∠A的正弦、余弦、正切和余切都叫做∠A的锐角函数。锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。初中数学主要考察正弦(sin),余弦(cos)和正切(tan)。正弦(sin)等于对边比斜边;sinA=a/c 余弦(cos)等于邻边比斜边;cosA=b/c 正切(tan)等于对边比邻边;tanA=a/b 余切(cot)等于邻边比对边;cotA=b/a
二、锐角三角函数公式 关于初中三角函数公式,在考试中用的最多的就是特殊三角度数的特殊值。如:sin30°=1/2 sin45°=√2/2 sin60°=√3/2 cos30°=√3/2 cos45°=√2/2 cos60°=1/2 tan30°=√3/3 tan45°=1 tan60°=√3[1] cot30°=√3 cot45°=1 cot60°=√3/3 其次就是两角和公式,这是在初中数学考试中问答题中容易用到的三角函数公式。两角和公式 sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB tan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA) 除了以上常考的初中三角函数公示之外,还有半角公式和和差化积公式也在选择题中用到。所以同学们还是要好好掌握。半角公式 sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2) cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2) tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA)) ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA)) 和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B) 2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B) sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgBsin(A+B)/sinAsinB - ctgA+ctgBsin(A+B)/sinAsinB
三、锐角三角函数图像和性质
四、锐角三角函数综合应用题 已知:一次函数y=-2x+10的图象与反比例函数y=k/x(k>0)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在
(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,-2a+10),B(b,-2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若BC/BD=5/2,求△ABC的面积. 考点:反比例函数综合题;待定系数法求一次函数解析式;反比例函数与一次函数的交点问题;相似三角形的判定与性质. 解答:解:
(1)把A(4,2)代入y=k/x,得k=4*2=8. ∴反比例函数的解析式为y=8/x. 解方程组y=2x+10 y=8/x,得x=1 y=8 或x=4 y=2,∴点B的坐标为(1,8);(2)①若∠BAP=90°,过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,对于y=-2x+10,当y=0时,-2x+10=0,解得x=5,∴点E(5,0),OE=5. ∵A(4,2),∴OH=4,AH=2,∴HE=5-4=1. ∵AH⊥OE,∴∠AHM=∠AHE=90°. 又∵∠BAP=90°,∴∠AME+∠AEM=90°,∠AME+∠MAH=90°,∴∠MAH=∠AEM,∴△AHM∽△EHA,∴AH/EH=MH/AH,∴2/1=MH/2,∴MH=4,∴M(0,0),可设直线AP的解析式为y=mx 则有4m=2,解得m=1/2,∴直线AP的解析式为y=1/2x,解方程组y=1/2x,y=8/x,得x=4 y=2 或x=?4 y=?2,∴点P的坐标为(-4,-2). ②若∠ABP=90°,同理可得:点P的坐标为(-16,-1/2). 综上所述:符合条件的点P的坐标为(-4,-2)、(-16,-1/2);(3)过点B作BS⊥y轴于S,过点C作CT⊥y轴于T,连接OB,如图2,则有BS∥CT,∴△CTD∽△BSD,∴CD/BD=CT/BS. ∵BC/BD=5/2,∴CT/BS=CD/BD=3/2. ∵A(a,-2a+10),B(b,-2b+10),∴C(-a,2a-10),CT=a,BS=b,∴a/b=3/2 ,即b=2/3a. ∵A(a,-2a+10),B(b,-2b+10)都在反比例函数y=k/x的图象上,∴a(-2a+10)=b(-2b+10),∴a(-2a+10)=2/3 a(-2*2/3a+10). ∵a≠0,∴-2a+10=2/3 (-2*2/3a+10),解得:a=3. ∴A(3,4),B(2,6),C(-3,-4). 设直线BC的解析式为y=px+q,则有2p+q=6?3p+q=?4,解得:p=2q=2,∴直线BC的解析式为y=2x+2. 当x=0时,y=2,则点D(0,2),OD=2,∴S△COB=S△ODC+S△ODB=1/2 ODCT+1/2ODBS=1/2*2*3+1/2*2*2=5. ∵OA=OC,∴S△AOB=S△COB,∴S△ABC=2S△COB=10. 以上就是初中数学锐角三角函数知识点总结,小编推荐同学继续浏览《初中数学知识点专题汇总》。对于想要通过参加初中数学补习班来获得优质的数学学习资源和学习技巧,使自身成绩有所提升的同学,昂...
已知锐角三角形的三边长分别为5 7 8求该三角形的面积
这个三角形的面积为:10√3。
解答过程如下:

如图,若AB=5,BC=8,AC=7,解答如下:
作AD⊥BC于D,
由勾股定理得AB²-BD²=AC²-CD²,
设BD=X,则CD=8-X,得
5²-X²=7²-(8-X)²
解得X=5/2,
∴AD=5²-(5/2)²=5√3/2
∴S△ABC=1/2BC*AD=10√3
扩展资料:
勾股定理:
在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。
(如下图所示,即a² + b² = c²)
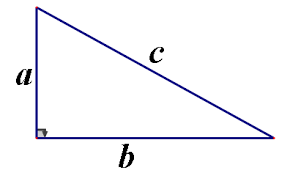
例子:
以上图的直角三角形为例,a的边长为3,b的边长为4,则我们可以利用勾股定理计算出c的边长。
由勾股定理得,a² + b² = c² → 2² +4² = c²
即,4 + 16 = 25 = c²
c = √25 = 5
三角形面积公式:
1、已知底和高:S=ah/2
2、两边一夹角:S=absinC/2
3、两角一夹边:S=(c^2sinAsinB)/[2sin(A+B)]
4、已知三条边:S=√p(p-a)(p-b)(p-c) 其中p=(a+b+c)/2
延伸阅读:
如何引导小学生推导三角形面积公式简介: 《三角形面积公式的推导》多媒体课件 本课件适宜于九年义务教育五年级数学(人教版)课堂教学,本课件从长方形面积计算公式入手。先让学生把长方形的纸剪成两个直角三角形,通...
三角形天气符号表示什么天气表示冰雹。 当地表的水被太阳曝晒汽化,然后上升到了空中,许许多多的水蒸气在一起,凝聚成云,此时相对湿度为100%,当遇到冷空气则液化,以空气中的尘埃为凝结核,形成雨滴(热带雨)或冰晶(...

什么是物流决策三角形物流三角形物流三角形是用来描述物流战略目标的模型,强调配销部份三者关系密切,相互权衡,以顾客服务为核心,并构成一物流网路。物流三角形的主体是客户服务目标,其中包含产品,物流...
立体三角形怎么折步骤步骤 准备一个正方形纸上,在任意颜色 最好政法面的是一个不同的颜色。理想的大小是20厘米x 20厘米。我将使用蓝色和白色的对立面: 玫瑰的颜色和意义: -红色:浪漫和爱情 -深粉红...
什么是直角钝角锐角图1、在几何学和三角学中,直角,又称正角,是角度为90度的角。它相对于四分之一个圆周(即四分之一个圆形),而两个直角便等于一个半角(180°)。 2、角度比直角小的称为锐角。 3、比直角...

锐角三角形直角三角形钝角三角形每个图形中三条高有什么特殊位置关锐角三角形的三条高都在三角形内部; 直角三角形的三条高有两条高与两条直角边重合,第三条高在三角形内部; 钝角三角形两个锐角顶点到对边的高在三角形外部,第三条高在三角形内部...

求三角形内角和教学反思三角形内角和教学反思 学生在上学期学角的时候,曾经量过三角板上每个角的度数。因此在这节课开始的时候,我先安排学生复习三角形的有关知识,再让学生画一个自己喜欢的三角形并...
三角形各个心的意义!三角形共有六心 内心:三条角平分线的交点,也是三角形内切圆的圆心。 性质:到三边距离相等。 外心:三条中垂线的交点,也是三角形外接圆的圆心。 性质:到三个顶点距离相等。 重心:三...
直角去判断一个角是锐角还是钝角数学二年级上:锐角与钝角教直角去判断一个角是锐角还是钝角数学二年级上:锐角与钝角教,如何运用信息技术使学生认识角的初步认识:·锐角直角钝角平角周角 2 教学设计 锐角直角钝角平角周角 2 教学设计 [...





