复变函数课程的有效教学策略

[例谈二次函数在闭区间上的最值问题]二次函数是高中数学中最基本也最重要的内容之一，而二次函数在某一区间上的最值问题，是初中二次函数内容的继续，随着区间的确定或变化，以及系数中参变数的变化，它又成为高考数学的...+阅读

复变函数课程的有效教学策略

摘要：复变函数是数学与应用数学专业本、专科的一门重要基础课程。

复变函数的性质定理多，概念抽象，学习难点多，由于受传统教学模式的制约，历来都存在难教难学的问题。

作者结合自己多年的教学经历，就在教学中如何改革教学模式，进一步提高教学效率，让学生全面系统地理解和掌握复变函数的理论和方法，并提出教学策略。

关键词：复变函数重点难点教学策略

引言

复变函数课程是高等师范大学和综合性大学数学类专业本、专科的一门重要基础课。

复变函数论主要研究对象是解析函数，是数学分析的后续课程，是实变函数微积分理论的推广和发展;复变函数论又称复分析，它不仅在内容上与实变函数微积分有许多类似之处，而且在研究问题方面与逻辑结构方面非常类似。

复变函数论不仅是我们所学数学分析的理论推广，而且作为一种强有力的工具，已经被广泛地应用于自然科学的众多领域，如理论物理、空气动力学、流体力学、弹性力学及自动控制学等，目前被广泛应用于信号处理、电子工程等领域。

作为高师数学专业复变函数课程的主讲老师，我在多年的教学实践中不断进行深入的思考、探索，积累了一些经验，在教学模式的改革方面进行了一些尝试，下面谈谈自己的教学体会。

1.加强复数基础知识教学

教材第一章主要讲有关复数及复变函数的基本概念，虽然学生在高中学过复数的基础知识，但由于该内容不是高考内容，中学数学教师对这部分内容一般都是略讲，大多数学生都没有学好;而这部分内容作为复变函数的基础知识，不仅是复变函数后续内容的学习关键，而且对学生以后从事中学数学教学很重要。

以前在复变函数的教学计划中，我们把第一章的课时安排为4～6课时，教学实践证明这个课时安排不合理，由于课时少，复数与复变函数的基础知识没学好，严重影响后面内容的学习，所以在近几年的教学中，我们一般都安排8～10课时，其目的是夯实基础，深刻理解复数和复变函数的有关概念，相关方法，重点理解幅角的无穷多值性、区域的有关概念及复数的几何表示，掌握复数的运算方法及复变函数的极限、连续的研究方法，为进一步学习解析函数打下良好的基础。

2.加强知识类比与同化

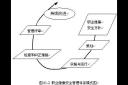
数学分析与复变函数相关知识结构对比：

从上面我们可以看出数学分析和复变函数的一些知识点的关系，复变函数是数学分析的后续课程，复变函数课程中有很多概念、性质、定理都是从数学分析平移过来的，因此，在复变函数教学时要加强与数学分析的联系，即利用学生已有的分析基础，发挥知识的迁移作用，促使知识的同化。

在复变函数的教学中，通过与数学分析中的相关知识作对比，可以把数学分析中的一些知识延拓到复变函数中。

比如数学分析中极限、连续、导数、微分、积分和级数有关概念、性质和定理都可以延拓到复变函数中，这样可以极大地提高教学效率，促进学生对复变函数理论与方法的理解和掌握。

例如在讲授复变函数极限概念的过程中可以与二元是函数的极限概念对比，利用实极限帮助学生对复极限的理解。

复变函数f(z)=u(x，y)+iv(x，y)的实部u(x，y)和虚部v(x，y)都是二元实函数，可以把复变函数的极限问题转化为数学分析中的二元函数的极限问题，利用不等式|u(x，y)||f(z)|，|v(x，y)||f(z)|，|f(z)||u(x，y)|+|v(x，y)|，可以得到结论：f(z)在一点z=x+iy有极限的充要条件是u(x，y)，v(x，y)这两个二元实函数在在该点的极限都存在。

3.抓住重点，注意知识的系统化

虽然复变函数是数学分析的后续课程，但复变函数不仅仅是数学分析的延拓，还有许多和数学分析不同的概念与方法，比如：多值函数、洛朗级数与孤立奇点、留数理论等。

在复变函数中学习的知识和数学分析中学习的知识侧重点也不一样，比如微分与导数，数学分析主要讲微分的概念、意义和计算，而在复变函数中，对于微分与导数的概念、性质及计算是一带而过，复变函数课程重点研究解析函数。

复变函数概念多，性质定理多，在教学过程中，既要抓好双基的教学，又要突出重点，更要通过总结、复习等教学环节，顺着知识的逻辑结构，理清知识脉络，这样才能让学生系统地掌握复变函数理论和方法。

例如：在教学柯西积分定理这一节时，柯西积分定理及推广一共有四个定理，教学总结时一定要理顺这四个定理的逻辑关系，即后面的定理包含前面的定理，并指出四个定理的本质是：f(z)在由周线(或复周线)C围成的区域内解析，并且连续到边界，那么?蘩■f(z)dz=0。

在复习周线积分?蘩■f(z)dz的计算时，可按下列顺序逐步判断并计算，若f(z)在C内不解析，则一般用参数法计算;若f(z)在C内解析且连续到边界，由柯西积分定理有?蘩■f(z)dz=0;若f(z)在C内有一个奇点，利用柯西积分公式计算;若f(z)在C内有多个奇点，则利用柯西留数定理计算。

4.改革教学模式，充分利用现代教学手段，突破教学难点

复变函数这门课程，历来都存在难教难学的问题，其主要原因：一是这门课程内容中存在一些较难的知识点。

比如：初等多值函数、柯西积分定理、解析函数的洛朗展式与孤立奇点等，这些概念、性质、定理抽象、思想方法复杂，学生难理解难掌握。

二是传统的教学模式以教师讲授为主，由于板书及语言表述的局限性，不能展现知识的变化过程，严重影响学生对知识的理解和掌握，满堂灌的讲授更是无法调动学生的学习积极性。

在教学中要改变传统的教学模式，利用现代媒体技术积极探索新的教学模式。

对于复变函数中的一些难点，我们一方面要充分利用现代教学手段，利用多媒体动态展示数学知识的发展过程及变化规律，另一方面要调动学生的学习积极性，让学生主动参与探究知识的活动，感悟知识的变化过程，掌握应用知识解决问题的方法，同时体会到领悟知识的愉悦，这样就能达到突破教学难点的目的。

结语

在复变函数课程的教学设计中，我们要改革传统的教学模式，积极探索有效的教学模式;用先进的教学理念指导教学设计，精心设计教学过程;在教学过程中既要让学生积极参与知识的探究过程，体验到学习的快乐，又要充分利用现代教学手段，突出教学重点，突破教学难点，这样就能实现三位一体的教学目标，使学生系统地掌握复变函数的理论和方法。

参考文献：

[1]钟玉泉.复变函数论[M].北京：高等教育出版社，2004.

[2]余家荣.复变函数[M].北京：高等教育出版社，2007.

[3]周鉴.对高师院校复变函数教学的思考[J].通化师范学院学报，2012，33(12).

[4]伍代勇.复变函数教学中的几点体会[J].安庆师范学院学报：自然科学版，2012，18(3).