[如何提升小学数学教学质量的策略]作为教师的我深深感到学习的重要性,在今后的教学中,我将立足于自己的本职工作,加强理论学习,转变教学理念,积极实践新课改,新目标,新理论,铺设好自己的专业化发展之路。下面是我对如...+阅读
你好 我今年也要参加高考,在最后的100天之中,是很关键的,尤其是前段时间,数学是很难攻上去的,首先要把书上的一些定理给吃透,学会运用,书上的题目 要牢牢掌握,之后要多做习题
一百来天的话, 题目是做不完的,我们要做就做经典的题目,选一些典型的题目做,不要什么题目都做,那不行 去网上搜索一些历年来最容易做错的题目
在此期间,自己要学会做笔记,准备错题本,反复看,思考,学会推算公式
典型例题一
例1下列图形中,满足唯一性的是( ).
A.过直线外一点作与该直线垂直的直线
B.过直线外一点与该直线平行的平面
C.过平面外一点与平面平行的直线
D.过一点作已知平面的垂线
分析:本题考查的是空间线线关系和线面关系,对定义的准确理解是解本题的关键.要注意空间垂直并非一定相关.
解:A.过直线外一点作与这条直线垂直的直线,由于并没有强调相交,所以这样的垂线可以作无数条.事实上这无数条直线还在同一个平面内,这个平面为该直线的一个垂面.
B.过直线外一点可以作一条而且仅能作一条直线与该直线平行,但可以作无数个平面和该直线平行.
C.过此点作平面内任一直线的平行线,这条平行线都平行于平面.所以过平面外一点与平面平行的直线应有无数条.
D.过一点作已知平面的垂线是有且仅有一条.假设空间点 、平面 ,过点 有两条直线 、 都垂直于 ,由于 、 为相交直线,不妨设 、 所确定的平面为 , 与 的交线为 ,则必有 , ,又由于 、 、 都在平面 内,这样在 内经过 点就有两条直线和直线 垂直,与平面几何中经过一点有县仅有一条直线与已知直线垂直相矛盾.
故选D.
说明:有关“唯一性”结论的问题,常用反证法,或者借助于其它已证明过的唯一性命题来证明.在本书中,过一点作已知平面的垂线有且仅有一条,同时,过一点作已知直线的垂面也是有且仅有一个.它们都是“唯一性”命题,在空间作图题中常常用到.
典型例题二
例2 已知下列命题:
(1)若一直线垂直于一个平面的一条斜线,则该直线必垂直于斜线在这个平面内的射影;
(2)平面内与这个平面的一条斜线垂直的直线互相平行;
(3)若平面外的两条直线,在这个平面上的射影互相垂直,则这两条直线互相垂直;
(4)若两条直线互相垂直,且其中的一条平行一个平面,另一条是这个平面的斜线,则这两条直线在这个平面上的射影互相垂直.
上述命题正确的是( ).
A.(1)、(2) B.(2)、(3) C.(3)、(4) D.(2)、(4)
分析:本题考查的三垂线定理及其逆定理的简单应用.应用这两个定理时要特别注意“平面内”这一条件,同时要注意各种不同位置的两定理的基本图形及其变式图形.
解:(1)已知直线不一定在平面内,所以不能用三垂线逆定理来判断垂直关系;
(2)平面内与这个平面的一条斜线垂直的直线必定与斜线在平面内的射影垂直,所以它们之间也平行;
(3)根据三垂线定理可证明直线与另一直线的射影垂直,但不能进一步说明直线和直线垂直;
(4)根据三垂线定理的逆定理和空间两直线所成角的概念,不难证明此命题的正确性.
故选D.
找些这样的例题 慢慢自己总结规律
要自己有耐心 千万不能急
祝今年的6月份 你能开出梦想之花 good luck
延伸阅读:
浅谈在小学数学教学中如何实施素质教育在小学数学教学中,我们应以素质教育为宗旨,以开发学生的身心潜能、提高学生的素质为核心,面向全体学生、全面提高教育教学质量,使学生的各种素质都获得培养和提高。小学数学素质...
如何有效应用信息技术提高小学数学教学课堂教学质量经验材料现代信息技术的广泛应用,正在对数学课程内容、数学教学、数学学习等产生深刻的影响,在数学教学中,充分运用信息技术,将图、文、声、像融为一体,使教学活动更加丰富多彩,让数学课堂...
一道高中数学立体几何的题目这应该是高中数学的附加题吧,(1)用基本方法,建系,找点坐标,代入计算。。(2)做fo垂直于mn于o点,然后求fo,mo长,最后勾股定理。 所以A'在ABCD上的投影是交点 不好意思,我看错了,你再等等,我...
求有关高中立体几何的数学题三角形ABC在平面a之外,AB∩a=P,BC∩a=Q,AC∩a=R,求证:P、Q、R三点共线。 解: 设三角形ABC所在的平面为b,由“一条直线上,若有两点在一个平面能,则该直线必在该平面内”知,直线AB,AC,...
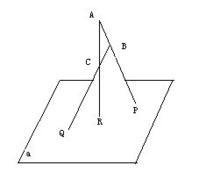
一道高中数学立体几何题解:(1):D,E是点A在PB,PC的射影。 ∴AD⊥PB,AE⊥PC ∠ABC=90° ∴CB⊥AB ① 且 ∵PA⊥平面ABC ∴PA⊥CB ② 结合①,②可得 CB⊥PAB ∴CB⊥AD 又 AD⊥PB ∴AD⊥平面PBC DE在平面PB...
高中数学立体几何题底面是正三角形,顶点在底面的射影是底面三角形的中心的三棱锥 根据定义来就行了! 1,4,可以证明,三个侧棱相等.且顶点在底面的射影是底面三角形的中心(由于是正三角形,四心合一). 2:...
小学数学教师应该如何有效进行课堂教学管理对教师来说,怎样使教学能力得以迅速提高,来适应教学要求,是一个至关重要的问题。教师都有系统的专业知识,对工作充满热情,干事业有决心;但是却常常被如何搞好课堂教学这个问题所困...
高中数学有哪几大重要模块1、三角变换与三角函数的性质问题; 2、解三角形问题; 3、数列的通项、求和问题; 4、利用空间向量求角问题; 5、圆锥曲线中的范围问题; 6、解析几何中的探索性问题; 7、离散型随机...

离高考还有一百天怎样很好的复习找个好的复习方法,一下《北京教学专家小组》吧,《北京教学专家小组》发表的2012高考资料和高考复习方法还有高考策略,针对以往考生都会遇到的老大难题,今年得到了彻底解决尤其是...





