[高三数学题目解析几何]解:设直线AB:y=kx+b,而k=tan45°=1,即直线AB:y=x+b. 联立直线方程和抛物线方程解方程组得点A,B的坐标,设A(x1,y1),B(x2,y2). 由抛物线:Y^2=4x,得:x=y^2/4.......(1) 将(1)代入直线方...+阅读
高中数学解析几何
72条 ∵在圆x2+y2=50上横坐标,纵坐标都是整数上的共有12个点:(1,7),(1,-7),(-1,7),(-1,-7),(7,1),(7,-1),(-7,1),-(-7,-1),(5,5),(5,-5),(-5,5),(-5,-5).
(1) 这12个点中可作60 条符合题意的直线ax+by-1=0(a,b不全为零),这些直线与圆x2+y2=50有二个横坐标,纵坐标都是整数的点:上面列出的12个点每二点可作一条直线,可作66条直线,但其中有6条直线过原点,它们分别为过:(1,7)、(-1,-7);(5,5)、(-5,-5);(7,1)、(-7,-1);(-1,7)、(1,-7);(-5,5)、(5,-5);(-7,1)、(7,-1),这6条直线不符合题意. (2) 过这12个点中的每个点都可作一条与圆x2+y2=50相切的直线,每条切线与圆x2+y2=50有且只有一个交点,这个交点的横坐标,纵坐标都是整数. 综上符合题意的直线ax+by-1=0(a,b不全为零)与圆x2+y2=50有公共点,且公共点的横、纵坐标均为整数的直线共有72条. 懂了吗? 希望能帮到你 O(∩_∩)O~
您好,是不是我的回答不详细,导致您不采纳呢? O(∩_∩)O~
高中数学立体几何
证明:
过s点向面abcd做垂线,交于点s1,过s1向bc边做垂线交于点s2,过s1向ab边做垂线交于点s3
以s1为原点,s1s3为x轴,s1s2为y轴,s1s为z轴建立空间直角坐标系
设ab为x,s1s为y,则s(0,0,y),a(x/2,-x/2,0),as【上加向右箭头】=(-x/2,x/2,y)
b(x/2,x/2,0),m(x/3,x/3,y/3),p(-x/6,x/6,2y/3),n(-x/3,-x/3,y/3),nm【上加向右箭头】=(2x/3,2x/3,0),pm【上加向右箭头】=(x/2,x/6,-y/3)
设面npm的法向量为i(注:i上面加向右箭头,我这儿打不出来,我写的这道题后面的i都带)
然后法向量垂直于nm,pm (相应位置相乘再相加的零)求出法向量 法向量与as对应成比例 所以SA//平面PMN
没时间了,明天来,要是没人接着我的写我在给你弄全
前面设i(a,b,c)
∵i⊥nm【上面加向右箭头后面的i都带】
i⊥pm【上面加向右箭头后面的i都带】
∴a*2x/3+b*2x/3=0
a*x/2+b*x/6+c*(-y/3)=0
∴(a+b)*2x/3=0∵x≠0∴a+b=0
∴x/3*a-c*y/3=0
∴ax=cy
∴b=-a,c=x/y*a
∴i=(a,-a,x/y*a)
i.【点乘】as=0
∴i⊥as
∴SA//平面PMN
解完了,应该没有问题,【法向量与as对应成比例】这句话我说的有问题,昨天着急,弄错了,你看解法就行
延伸阅读:
哪位大事能给我归纳一下高中数学解析几何啊椭圆双曲线抛物线椭圆的方程是x2/a2+y2/b2=1 这里是加号,不要和双曲线的减号搞混了。然后这里的a是大于c的。双曲线里的a是小于c的。所以椭圆中c2=a2-b2而双曲线中c2=a2+b2的(这点细节很多人都...
高中数学文科如何才能学好解析几何要学好高中数学的解析几何,就要会用好的学习方法.. 以下是我COPY的一些方法... 希望对你有用... 数学是必考科目之一,故从初一开始就要认真地学习数学。那么,怎样才能学好数学...
高中解析几何和立体几何部分1.恶补基础知识; 2.做大量练习; 3.不断地问你周围的高手,学习他们的思考方式,学习方法和学习习惯; 4.永远不要觉得140分很遥远,要坚韧,有毅力,相信自己能补上去; 5.提过一次,然后坚持...
高三数学解析几何设M(x1,y1),N(x2,y2),Q(1,0),依题意,直线PA经过点A(-2,0),P(4,t),可以设AP:y=t6(x+2),(6分) 和圆x2+y2=4联立,得到y=t6(x+2)x2+y2=4,代入消元得到,(t2+36)x2+4t2x+4t2-144=0,(7分)...
一道高中数学立体几何的题目这应该是高中数学的附加题吧,(1)用基本方法,建系,找点坐标,代入计算。。(2)做fo垂直于mn于o点,然后求fo,mo长,最后勾股定理。 所以A'在ABCD上的投影是交点 不好意思,我看错了,你再等等,我...
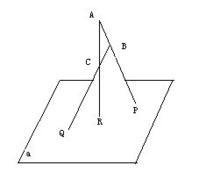
求有关高中立体几何的数学题三角形ABC在平面a之外,AB∩a=P,BC∩a=Q,AC∩a=R,求证:P、Q、R三点共线。 解: 设三角形ABC所在的平面为b,由“一条直线上,若有两点在一个平面能,则该直线必在该平面内”知,直线AB,AC,...
一道高中数学立体几何题解:(1):D,E是点A在PB,PC的射影。 ∴AD⊥PB,AE⊥PC ∠ABC=90° ∴CB⊥AB ① 且 ∵PA⊥平面ABC ∴PA⊥CB ② 结合①,②可得 CB⊥PAB ∴CB⊥AD 又 AD⊥PB ∴AD⊥平面PBC DE在平面PB...
高中数学立体几何题底面是正三角形,顶点在底面的射影是底面三角形的中心的三棱锥 根据定义来就行了! 1,4,可以证明,三个侧棱相等.且顶点在底面的射影是底面三角形的中心(由于是正三角形,四心合一). 2:...
高三数学二轮复习教学案例解析几何综合题去文库,查看完整内容>内容来自用户:吴美良高三数学二轮复习教学案例------解析几何综合题 一、知识点概括:解析几何综合题是高考命题的热点内容之一.这类试题往往以解析几何知...





